El teósofo español
Mario Roso de Luna hizo el siguiente análisis geométrico de uno de los símbolos
que se utiliza en el sello de Salomón:
« Entre los diversos símbolos comentados en el trabajo del Sr. Urbano sobre el
Sello de Salomón (link) el más antiguo ó de filiación menos conocida y que parece prestarse a
interpretaciones y desarrollos geométricos innumerables pero fáciles de
evidenciar, es el siguiente:
En este símbolo vemos multitud de figuras y elementos
geométricos tales como:
-
el cuadrado con sus dos
diagonales DC y BE;
-
los dos triángulos
isósceles ABC y DEF cuyos ápices respectivos A y F están cada uno en el punto
medio de la base del otro;
-
los ocho triángulos rectángulos ó isósceles DEB ,
DEC, BCE , BCD , DOE , EOC, COB , BOD ;
-
los dos triángulos
isósceles GDB y HEC que con los anteriores suman doce triángulos isósceles;
-
otros doce triángulos escalenos tales como el AID y
AKE, DIG y EKH;
-
un rombo AGFH;
-
dos rectángulos DAFB y
AFCB;
-
y dos cuadriláteros no
paralelográmicos OIGL y OKHM.
Reproduzcamos la figura sombreando la estrella de seis
puntas que aparece inscripta en el rectángulo DECB.
Quedan así al exterior de dicha estrella cuatro
triángulos escalenos iguales entre si (dos arriba y dos abajo) y otros dos
triángulos laterales é isósceles también iguales entre sí.
Pues bien, la estrella de seis puntas inscripta se la puede
considerar formada por la superposición de estas dos figuras, que además de yuxtaponerse
en el símbolo de una manera idéntica a los dos triángulos del sello salomónico,
forman cada una de por sí la figura geométrica llamada cuadrilátero completo
por los geómetras modernos.
Y la importancia de este cuadrilátero completo en la
antigüedad sacerdotal debió ser no menos inmensa que la que goza en nuestra geometría
actual. Sobre ella debieron existir tratados especiales de geometría superior
en la biblioteca de Alejandría, pues ya aparece en los fragmentos de la “Colección
Matemática” de Pappus, un gnóstico que vivió en dicha ciudad a fines del siglo
IV y que probablemente la aprendió de los grandes geómetras que fueron sus
predecesores.
En el caso especial de la regularidad de cualquiera de las
dos figuras anteriores los dos triángulos superpuestos ABK y ACI ó bien FDM y
FEL son iguales entre sí, pero para formar en todo otro caso, distinto de este
caso límite, la figura del cuadrilátero completo, sin semejante restricción,
bastan dos triángulos cualesquiera superpuestos por un ángulo igual, aunque sus
otros dos ángulos y sus tres lados respectivos no sean iguales, como se ve en
la figura.
Este cuadrilátero completo formado por la superposición
de los dos triángulos ABE y ACD que tienen un ángulo A igual, puede
considerarse también formado por un sistema de cuatro rectas cualesquiera que
se cortan de dos en dos y asimismo por la prolongación hasta su encuentro de
los lados opuestos de un cuadrilátero ordinario cualquiera, tal como el ADFE, y
de aquí le viene el nombre de cuadrilátero completo.
La geometría moderna considera en el cuadrilátero
completo seis vértices ó puntos de intersección A, B, C, D, E y F y tres
diagonales BC, DE y AF, que unen dos a dos, los tres pares de vértices
opuestos.
En realidad esta prodigiosa figura, pese a su elemental
aspecto, define por sí sola, entre los infinitos puntos y las infinitas rectas
de su plano, una multitud de puntos y rectas singulares ó únicas, que en dicho plano
gozan de una determinada propiedad. Y esto demuestra hasta la evidencia la
importancia del cuadrilátero completo como uno de los más preciosos símbolos
que nos legase la sabiduría de la antigüedad.
Ya que en efecto, el cuadrilátero completo define:
·
1 recta, única diagonal
exterior del cuadrilátero que une los ápices B y C de los dos triángulos
superpuestos.
·
2 rectas, únicas diagonales
interiores AF y DE del cuadrilátero completo.
·
3 rectas, únicas
diagonales del cuadrilátero.
·
4 rectas, únicos lados
del cuadrilátero cortándose de dos en dos.
·
5 rectas, gráficas que
se ven en la figura formada por los cuatro lados y la diagonal exterior.
·
6 rectas, ó sean los
cuatro lados y las dos diagonales interiores.
·
7 rectas, número total
de rectas laterales y diagonales del cuadrilátero completo.
·
8 rectas, las anteriores
y la formada por los puntos medios de las tres diagonales que la geometría
demuestra están siempre en línea recta.
·
9 rectas si se agrega a
las anteriores el eje polar único común a los tres círculos descriptos sobre
las tres diagonales como diámetros.
·
10 rectas, si se considera
además el eje radical común y único para dichos tres círculos.
·
11 a 13 rectas, si además
se consideran las tres rectas polares de los repetidos círculos tomadas de dos
en dos.
·
14 rectas, ó sean los
cuatro lados, las tres diagonales, las tres polares y los tres ejes radicales
de los repetidos
círculos tomados de dos en dos.
·
15 rectas, las del
número anterior y el eje polar ternario común a los tres círculos dichos.
·
16 rectas, ó sean las
anteriores y el eje radical ternario.
·
22 rectas, si a las
anteriores se agregan las seis alturas de los dos triángulos.
·
De 22 a 28 rectas, si se
consideran además las seis medianas de los dos triángulos.
·
De 29 a 33 rectas, si se
considera además la bisectriz común del ángulo A y las otras cuatro de los dos
triángulos.
·
34 rectas, sí se
considera además la recta en el infinito que juega a veces en las demostraciones
del cuadrilátero.
·
35 y 36 rectas, con las
dos tangentes comunes exteriores de los círculos descriptos sobre las dos
diagonales interiores como diámetros, círculos que se cortan siempre.
·
De 37 a 42 rectas, con
las cuatro tangentes comunes exteriores al círculo descripto sobre la diagonal
exterior como diámetro y a cada uno de los dos citados anteriormente.
·
De 42 a 54 rectas, con
las anteriores y las seis tangentes comunes exteriores a los tres círculos
inscriptos en cada uno de los dos triángulos que forman el cuadrilátero
completo, tomando dichos círculos de dos en dos.
·
De 54 a 68 rectas, con
las tangentes comunes exteriores al círculo de Euler, al inscripto y a los
ex-inscriptos en el triángulo y a los descriptos sobre las tres diagonales como
diámetros.
No seguiremos investigando acerca de alguna otra recta
singular que acaso se caracterice y determine igualmente en su plano por el cuadrilátero.
Pero como en la figura origen de esta nota se ven no uno
sino cuatro cuadriláteros
completos: A I O K B C , F L O M D E , O I G L D B y O K H M E C, puede asegurarse, en resumen, que dicho símbolo entraña la
determinación, por lo menos en el plano de 1 a 272 rectas únicas del plano que
gozan de cierta propiedad exclusiva y característica, siquier, y dada la
disposición regular de la figura, algunas pocas de ellas confundan sus segmentos
en una recta común, cosa que en la misma figura, hecha irregular, no
acontecería.
Además, y dado el llamado principio de correlación, que es la base de la geometría superior
de Mr. Charles de la que después hablaremos, podemos también hallar
determinados por el cuadrilátero completo deducido de nuestro símbolo, los
siguientes puntos que gozan de determinada propiedad dentro de los infinitos
del plano y que gozan de la propiedad también de ser correlativos de las rectas
indicadas anteriormente, aunque no vayan expuestos por signos de orden de correlación
con aquéllas.
·
1 punto, vértice único
común a los dos triángulos superpuestos.
·
2 puntos, vértices
únicos exteriores del cuadrilátero completo.
·
3 puntos, los tres
vértices antes expresados.
·
4 puntos, los cuatro
vértices del cuadrilátero ordinario que es núcleo del cuadrilátero completo.
·
5 y 6 puntos los
anteriores y los vértices extremos B y C.
·
7 puntos, el total do
vértices del cuadrilátero completo con más el punto de intersección de las dos
diagonales interiores.
·
8 a 11 puntos, ó sean los
anteriores y los puntos medios de las tres diagonales que están siempre en
línea recta.
·
12 puntos, si a los
anteriores se agrega el polo único común a los tres círculos descriptos sobre
las tres diagonales como diámetros.
·
13 puntos, que son los
expresados y el centro radical común a dichos tres círculos.
·
De 14 a 17 puntos, sí se
agregan los polos de los tres círculos dichos, tomados de dos en dos.
·
De 17 a 19 puntos, ó
sean los anteriores y los centros radicales comunes a dichos tres círculos de
dos en dos.
·
21 puntos, los anteriores
y los de intersección de la diagonal exterior con cada una de las dos
diagonales interiores.
·
De 22 a 28 puntos, los anteriores
y los seis pies do las seis alturas de los dos triángulos del cuadrilátero.
·
De 28 a 34 puntos, con
los pies de las seis medianas de los dos triángulos dichos.
·
De 34 a 42 puntos, con
los pies de las seis bisectrices de los mismos.
·
De 40 a 48 puntos, con
los dos centros de los dos círculos
inscriptos y los seis circunscriptos a los dos triángulos.
·
De 48 a 52 puntos, con
los cuatro centros del círculo de 9 puntos de Euler ó del de 12 puntos de
Feuerbach, para los dos triángulos que forman el cuadrilátero completo y para
los dos triángulos de diferencia entre éste y el cuadrilátero ordinario
generador.
Y si hubiéramos seguido con más fidelidad la ley de
correlación, se habrían aumentado no pocos puntos y rectas más a los ya dichos.
Los puntos considerados suponen pues, para los cuatro
cuadriláteros completos del símbolo que nos ocupa, 272 puntos correlativos a
otras tantas rectas, ó en suma, un mínimo de 544 puntos y rectas del plano que
gozan de una propiedad característica.
Considérense ahora los innumerables teoremas geométricos
que con elementos tan múltiples se pueden formular, y se adquirirá la evidencia
de que la figura en cuestión es de las más sintéticas y augustas que la sabia
antigüedad perdida nos ha podido transmitir después de un largo periodo de
oscurantismo.
Ya que esta figura, en efecto, es clara geométrica, a la
par antigua y moderna, como que ningún geómetra ignora que por el cuadrilátero
completo se explican sintéticamente todas las teorías de la geometría elemental
analítica ó sintéticamente y otras ya menos elementales, tránsito a la novísima
geometría superior, tales como:
- Los conjugados anarmónicos y armónicos.
- Las series de puntos.
- Las series de rectas.
- Los haces de planos.
- La teoría proyectiva.
- Las figuras homológicas y homotétícas.
- La teoría de polo y polar en el círculo y el elegante método de las polares recíprocas.
- Las figuras semejantes, y dentro de ellas los casos especiales de igualdad.
- La teoría de los ejes y centros radicales para el círculo.
- Las figuras inversas.
- El método de transformación geométrica por radios rectores recíprocos.
- El círculo de Euler ó de los 9 puntos ó el de Feuerbach de los 12 puntos, a saber: los puntos medios de los tres lados de todo triángulo, los pies de sus tres alturas, los tres puntos medios de las distancias del punto de concurso de las tres alturas: a los tres vértices del triángulo y los cuatro puntos de tangencia respecto del círculo inscripto y de los tres ex-inscriptos en el triángulo dicho.
Y algunas otras teorías menos importantes que abarcan
toda la síntesis de la geometría del plano y de la radiación y son la base
primera para el estudio de la perspectiva, invento felicísimo que nos permite a
su vez estudiar en el plano todas las relaciones del espacio.
El conocimiento de la geometría viene desde tiempos muy antiguos
Quien quiera convencerse por si mismo de la exactitud de
cuanto decimos, puede verlo desenvuelto en el meritísimo apéndice 9 del libro
III del “Tratado de Geometría elemental” de Eugène Rouché y Charles
de Comberousse, a quien para mayor demostración de nuestros asertos seguimos
con la mayor fidelidad en el presente artículo.
Y tomándose la molestia de meditar sobre dicho apéndice,
cuanto sobre el profundo prefacio de la obra, ó leyendo los artículos de Mackey
en la “Chamber’s Encyclopedia”, ó las investigaciones de George Biddell Airy y de Francis
Baily acerca de la astronomía antigua, se adquirirá la
convicción de que el saber perdido de Egipto y de India, alcanzaba a todos los
problemas de
la ciencia geométrica pura y aplicada en un grado de
desarrollo, igual
por lo menos al tan alto de que el mundo occidental
moderno se
vanagloria.
Es verdad que leyendo dicho prefacio parece como que a
medida que han transcurrido los siglos se han ido acumulando las conquistas geométricas
hasta la prodigiosa florescencia de hoy en día, pero lo que hay de real en este
fenómeno es el hecho de que grandes periodos de barbarie han sepultado excelsas
civilizaciones con todos sus tesoros científicos, y cuyo ulterior, lento y
gradual redescubrimiento ha sido difícil debido a que no se trata de objetos materiales
sino de ideas ó cuanto más, de libros, constituye nuestra ciencia actual, la
ciencia de nuestro ciclo.
¡Qué diría el filósofo Vico entre aquel período de barbarie pasada y otro
más ó menos lejano de barbarie futura!
Hay entre el progreso de la ciencia positiva moderna y la
formación de los árboles genealógicos, un manifiesto paralelo. Y partiendo
aquélla de un principio común, felizmente salvado del naufragio y de un tronco
común, éstos han ido desarrollándose, dividiendo y subdividiendo su ramaje
inmenso.
Pero en uno y en otro árbol existe un fenómeno de estrabismo,
ya que lo tomamos sólo en un sentido que es hacia nosotros, y cuando lo
consideramos en sentido inverso ó hacia el pasado, entonces los conceptos
cambian y aquel único tronco del principio salvado es mera rama de todo un
sistema científico transcendente, como aquel único tronco genealógico, origen
de nuestro árbol genealógico resultamos proceder de 2 padres, 4 abuelos, 8
bisabuelos, 16 tatarabuelos, 32, 64, 128, 256, etc., ascendientes de grado
ulterior.
El verdadero árbol histórico resulta así invertido a
nuestra vista, y en cuanto a lo humano, sus múltiples ramas de millares de antepasados,
según la progresión geométrica nos hacen a las humanidades pretéritas
solidarias por entero de la traída a la vida de cualquiera de nosotros.
Pero todo este vasto conjunto de ascendientes no hacemos
nuestra historia más que con aquellos que por la índole singular de sus hechos se
hiciesen perdurables en el recuerdo. De igual modo entre las innumerables
verdades geométricas resumidas en los símbolos típicos paseados por toda la
antigüedad, tales y tan excelentes como el Sello de Salomón, síntesis de todos
ellos, sólo encontramos algunos, pocos, aquí y allá esparcidos en trabajos
fragmentarios y de discípulos de discípulos, alterados acaso en su excelsitud
prístina, pero suficientes a desprender luz al choque con el genio que
investigue entre sus ruinas.
Huygens, Poncelet y Charles, en efecto, pueden
considerarse los tres grandes reveladores de la geometría tal y como hoy se nos
presenta, pero para ello ha sido preciso que Huygens fuese previamente, según
el dicho de Newton, el más perfecto y el más excelso imitador de los antiguos. (Esto
se menciona en el prefacio de la obra citada).
En cuanto a Poncelet, su clásico “Tratado de las
propiedades proyectivas” que es la base de la geometría de posición, no tiene
otro fundamento que el de dos teoremas atribuidos a Desargues, matemático del
siglo XVII, pero los que se hallaron por éste en el “Tratado de los Porismos”
de Euclides, matemático del siglo III a. de C., quien a su vez, según Ronché y
Comberousse, resumiendo los descubrimientos de sus antecesores y los suyos
propios, reunió la escuela platónica a la de Alejandría y así preparó la obra
de sus sucesores.
Y semejantes antecesores no eran otros que Platón (del siglo
V a. de C.), quien escribió en el frontispicio del Liceo: “que nadie entre que
no sepa de geometría”; y su maestro Pitágoras de Samos (del siglo VI a. de C.) y
cuya escuela fuera la continuación de la Jónica de Tales de Mileto, que unos
seiscientos a setecientos años antes de nuestra Era importase en Grecia la
geometría aprendida durante su iniciación en los templos de Egipto. Templos
cuya sabiduría convive con la cuna de la humanidad a través de ciclos perdidos
que hoy se toman como mitológicos más que históricos.
En cuanto a Mr. Charles, dicen los mismos autores que:
« Un pasaje obscuro de los Porismos de Euclides y algunos
lemas del antiguo Pappus (siglo VI) —lemas probablemente inspirados en el
estudio de este y de otros tesoros alejandrinos, aunque para nosotros ya perdidos—
lo ha conducido felizmente hacia su geometría superior, adivinando en ellos
algo muy grande que en vano pusiese a prueba la sagacidad de las más ilustres
inteligencias de los últimos siglos. »
Y hasta las mismas videncias del matemático Monge (del siglo
XVIII) al fundar la geometría descriptiva, se debió a lo familiarizado que
tenía su espíritu con las enseñanzas de aquellos clásicos, haciendo ver la
íntima alianza de las figuras planas y las del espacio, sentando así el
principio de las llamadas relaciones contingentes ó de continuidad, por las que
se consideran indiferentemente como redes ó como imaginarias todas las diversas
partes de la figura, con lo cual la vieja geometría métrica penetró de lleno en
el excelso mundo de lo abstracto, de lo por decirlo así, sin forma.
La geometría de Pitágoras y Platón, aun considerando sólo
los fragmentos de ella que han llegado hasta nosotros, abarcaba ya el famoso teorema
del triángulo rectángulo, cuyos gráficos han sido ya apuntados en el texto que
comentamos; la teoría de los sólidos regulares, la de los máximos y mínimos
superficiales y volumétricos; el fecundo método de los lugares geométricos; el fecundísimo
llamado analítico ó algebraico y la teoría de las secciones del cono; círculo,
elipse, parábola é hipérbola, con sus diferentes propiedades, desenvuelta luego
por Apolonio (quien vivió en el siglo III a. de C.) y aplicadas a la
astronomía.
Es decir que sin contar la parte mayor perdida ó secreta y
objeto sólo de iniciaciones superiores, no desmerecía la geometría importada de
Egipto por los griegos de nuestra presente geometría.
Conocidas son también las tentativas de Simpson
(1717-1785) para descifrar la parte ignota de los Porismos de Euclides, aunque
los verdaderos continuadores de la gran obra Pitagórica son Arquímedes (287-212
a. de C.), Apolonio (247 a. de C.), Hiparco (150 a. de C.), Menelao y Tolomeo
con la trigonometría de su Almagesta, en el siglo I y II d. de C., y finalmente
la escuela de Bagdad que en el siglo IX y que comentó con gran fruto los
escasos restos salvados del incendio de la Biblioteca de Alejandrina.
Más análisis geométrico sobre la figura
Las relaciones numéricas entre los múltiples elementos
integradores del cuadrilátero completo encerrado en el símbolo que comentamos,
acaso no están apuradas aún por nuestra moderna geometría.
Al ser ellas síntesis de nuestros más altos conocimientos
geométricos, son a la vez síntesis y compendio también del universo objetivo,
ya que aunque empezamos a conocer las leyes que rigen a la fenomenología del
Cosmos mediante la observación y la experiencia, es por demás sabido que las
ciencias positivas no revisten verdadero carácter de generalidad hasta que no
caen dentro de la férula matemática que las sintetiza, como se ve con la
mecánica racional, la física matemática, la física química, etc., etc.
Es soberanamente curioso el que las proposiciones
fundamentales del cuadrilátero completo se hallen ya en autores antiguos con
cuyos mutilados redescubiertos van encontrando los geómetras modernos suscitaciones
para los desarrollos más fecundos. Así vemos que el teorema de que «en todo
cuadrilátero completo cada diagonal prolongada queda dividida armónicamente por
las otras dos», es la proporción número 129 de la “Colección Matemática” de Pappus, y se
sabe que se llamaba armónica a la relación:
que se determina en cada diagonal según aquel teorema
porque constituía la base de la teoría platónica de los tonos musicales, teoría
que desgraciadamente no ha llegado hasta nosotros, pero que, como se ve, tenía
una base geométrica, también comprendida en el símbolo salomónico.
Llamar geométrica a dicha base, equivale a llamarla
matemática. No distaría pues tanto de la teoría musical numérico-vibratoria
moderna, ni sería tan artificiosa como el frívolo juzgar de algunos imaginara
caprichosamente.
Existe toda una geometría novísima sobre las relaciones
anarmónicas y armónicas que se derivan del estudio del cuadrilátero completo. El
desarrollarlas, sobre todo para los no iniciados en estas alturas geométricas,
daría a esta nota proporciones de libro, cuando además pueden verse en el
apéndice citado ó en algunas obras similares.
Pero no podemos menos de indicar algunas ideas
fundamentales.
La llamada relación anarmónica de cuatro puntos A, B, C y
D de una recta es el cociente de las relaciones de las distancias de dos
cualesquiera de estos puntos C y D, por ejemplo, a los otros dos, ó sea:
en donde x representa un valor que
varía a medida que C y D se mueven de un modo cualquiera el uno entre A y B y
el otro fuera del segmento AB.
Claro es que estos valores varían según la respectiva
posición de C y D con respecto a A y B.
Pero entre todos estos valores hay 4 singulares,
considerando ahora fijos a A, B y C y móvil sólo a D, a saber:
- Cero cuando D pasa sobre B.
- Infinito cuando pasa sobre A.
- Uno cuando pasa por C (colocado en el punto medio de A y B como le hemos supuesto en la figura).
- Y menos uno cuando los puntos C y D (considerado de nuevo C como variable) se hallan en una excepcional posición, tal y como los puntos P y Q de la figura, determinados por la prolongación de las dos diagonales del cuadrilátero completo sobre la tercera, como ya decimos al hablar de la proposición 129 de Pappus.
 Sobre un haz de cuatro rectas OA, OB, OC y OD, cortados
por una recta móvil cualquiera M se pueden hacer idénticas consideraciones, de
las que resultan las relaciones anarmónicas de un haz de cuatro rectas, ó sean
las relaciones anarmónicas de los cuatro puntos que este haz determina sobre
una transversal cualquiera (M ó M'), relaciones cuyo valor es constante y
bastan para caracterizar el haz.
Sobre un haz de cuatro rectas OA, OB, OC y OD, cortados
por una recta móvil cualquiera M se pueden hacer idénticas consideraciones, de
las que resultan las relaciones anarmónicas de un haz de cuatro rectas, ó sean
las relaciones anarmónicas de los cuatro puntos que este haz determina sobre
una transversal cualquiera (M ó M'), relaciones cuyo valor es constante y
bastan para caracterizar el haz.Ellas admiten los mismos casos singulares antes expuestos
y llevan por la mano a todos los teoremas de homología ó involución, según
demuestra el “Tratado de Geometría superior” de Mr. Charles, apoyada en otra
proposición de Pappus, la número 322, también derivada del cuadrilátero
completo y acerca de la cual dice el mismo autor en su prólogo:
« Ninguna proposición me parece tan adecuada para descubrir
relaciones ó demostrar propiedades en una figura; hasta el misino teorema de la
proporcionalidad entre los lados de dos triángulos semejantes supone la
consideración lineal, auxiliares que rara vez aparecen entre los datos de la
cuestión, mientras que las relaciones anarmónicas se presentan casi siempre en la
figura misma o pueden formarse muy fácilmente. »
Nunca se ponderará bastante, en efecto, la teoría de las
relaciones anarmónicas y la de las armónicas como caso especial suyo, porque permiten
hacer lo que se ha llamado geometría por partida doble ó sean series dobles de
teoremas correlativos, sin más que substituir los conceptos de recta y punto recíprocamente
en los enunciados.
Vaya un ejemplo de esta correlación de enunciados en los
dos teoremas de
Desargues que antes citáramos como base del “Tratado de las propiedades proyectivas” de Poncelet, y que demostrado el
uno, el otro queda demostrado también:
|
Teorema Cuando dos triángulos tienen sus vértices situados dos a dos en tres rectas que concurren en un mismo punto, sus lados se cortan dos a dos en 3 puntos situados en línea recta. |
Teorema Cuando dos triángulos son tales que sus lados se cortan dos a dos en tres puntos situados en línea recta, sus vértices están situados dos a dos en tres rectas que concurren en un punto. |
Esta
teoría es base de multitud de teoremas aplicables al círculo, tales como los
siguientes:
A)
La relación anarmónica constante de cuatro puntos fijos de una circunferencia
respecto de otro quinto punto que sobre ella se mueva y su correlativo de la
relación anarmónica constante de las cuatro tangentes, respecto de una quinta
móvil.
B)
En todo hexágono inscripto los tres pares de lados opuestos se cortan dos a dos
en tres puntos que están en línea recta (teorema de Pascal) y su correlativo
(teorema de Briandson), y de que en todo hexágono circunscripto las tres
diagonales que unen los vértices opuestos concurren en un punto.
C)
Todos los problemas de tangentes y puntos de tangencia a uno, dos o tres
círculos están estrechamente ligados, en fin, con las relaciones anarmónicas
desprendidas del cuadrilátero completo.
D)
La aplicación adecuada de los dos teoremas mencionados en (B) a todo pentágono,
cuadrado y triangulo inscriptos y circunscriptos, por ser ellos hexágonos con
uno, dos ó tres lados reducidos a un valor cero, conclusión que abarca para el
triángulo al principio de que las tres medianas concurren en un punto, las tres
alturas en otro punto y las tres bisectrices en otro, puntos estos tres últimos
que se confunden en uno en cada uno de los dos triángulos equiláteros del sello
salomónico, por ser idénticas y confundirse a su vez, las medianas, alturas y
bisectrices rectas que cada una de ellas es triple por tal razón, a la manera
de como es triple también el centro del círculo considerado como punto límite
de los focos y de la distancia media de los focos de una elipse cuya
excentricidad se ha reducido a cero.
~ * ~
Las
tan importantes conclusiones a las que nos conduce el considerar como hexágono a todo polígono de un número de lados inferior (cinco, cuatro ó tres); las
propiedades de excepcional regularidad, por decirlo así, del hexágono regular
(tales como el ser su lado igual al radio y su apotegma la mitad del radio,
constituir el triángulo equilátero con sus vértices alternados y el rombo con
dos de sus lados y los radios correspondientes), son una prueba más de la
importancia del número seis, etcétera, en la naturaleza, seis que con el uno, el centro, el ignorado ó incognoscible, constituye ese Sagrado y Abstracto siete
reflejado tanto en todos los símbolos que el Sr. Urbano con tanta sagacidad ha
recogido, cuanto en todas las correlaciones que análogamente encuentra en lo
infinitamente grande y lo infinitamente pequeño nuestro tratadito “Evolución
solar y series astro químicas” [Évolution
solaire et series astrochimiques] (París, 1906).*
Por
ser ya de geometría más elemental renunciamos a demostrar de qué modo la
combinación de posiciones de dos triángulos isósceles, de los que vemos en la primera
figura, pueden aplicarse para la formación de multitud de figuras demostrativas
de teoremas sobre bisectrices perpendiculares, oblicuas y paralelas, etc., etc.
Lo
apuntado creo basta a la cumplida demostración relativa de la importancia del
símbolo referido, y todas ó casi todas las propiedades apuntadas respecto del
cuadrilátero completo son aplicables, por otra parte, como es sabido, al plano y
al espacio.
(*
Nota: sin pretender extractar dicho trabajo, diremos sólo que en el se demuestra
la coexistencia en el sistema planetario de una serie de seis planetas
pequeños, otra de seis planetas grandes y otra de seis tipos de soles; la
correlación serial con otras seis series ó evoluciones de los átomos y sus pesos
proporcionales; la correlación serial por seis en los dos grupos de satélites
grandes y pequeros de Júpiter y Saturno y otra multitud de consideraciones
concordantes que demuestran al número seis como formador del macrocosmos y del
microcosmos. Y también este hecho debió de ser conocido en la antigüedad a
juzgar por los diversos mitos de los seis dados de Baco, etc., etc.) »
(Sophia, octubre de 1907, p.366-375)





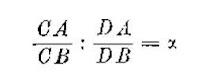
Cid podrías pasarme el link o pdf sobre aptitudes, valores que han de tener y cultivar aquellos que quieran ser teosofos. Esa mini entrada para aquellos que quieran adentrarse en la teosofia, por favor. Gracias
ResponderBorrarLos valores para ser teósofo son los mismos que te piden las religiones (bondad, fraternidad, etc.), pero si te refieres los requisitos para poder volverse un discípulo de los maestros, Blavatsky los mencionó en este otro capítulo:
Borrarhttps://esoterismo-guia.blogspot.com/2021/01/discipulos-chelas-laicos.html
Cid, en el artículo sobre discípulos y chelas se expone esto.
ResponderBorrar“Y el chela no solamente es llamado a encarar todas las proclividades malas latentes en su naturaleza, sino también todo el poder maléfico acumulado por la comunidad y la nación a las cuales pertenece, ya que él es parte integrante de esos agregados y lo que influencia al ser humano individual o a la colectividad (ciudad o nación), repercute también sobre él.
Y en este caso, la batalla que ha librado en favor de la bondad, desarmoniza todo el conjunto de la maldad en su ambiente, la cual reacciona precipitando su furia sobre él.
Un humano que está satisfecho con seguir la corriente de sus semejantes, siendo casi como ellos, quizá un poco mejor o algo peor de lo ordinario, no atraerá la atención de nadie. Pero tan pronto como se sabe que ha podido detectar la vaciedad del teatro de la vida social, su hipocresía, egoísmo, sensualidad, codicia y otros aspectos negativos, y ha tomado la determinación de levantarse a un nivel superior. Entonces inmediatamente se convierte en el objeto de odio y toda naturaleza negativa, fanática o malévola, que le envían una corriente de malquerencia que se opone a su poder de voluntad.”
Significa que, ¿debemos encarar sin miedo y sin cobardía los conflictos que afectan a nuestro país/pueblo/comunidad sin miedo a pesar de que ello pueda generar emociones y pensamientos negativos hacia nosotros en nuestro entorno hasta incluso llegar a sufrir daño físico para llamar la atención de los mahats?
Es decir tener iniciativa y dejar ir la libertad que hay en nuestro interior sin importar las consecuencias. Por ejemplo: españa sufre de nacionalismo y los pueblos de una parte del territorio están contaminados de odio, resentimiento, envidia etc…
En este caso, ¿podría escribir una carta para los habitantes del pueblo, para concienciar sobre lo que es el nacionalismo y lo que ha degradado sus vidas?, ¿se refiere a esto? En tener iniciativa sin miedo y sin importar lo que devenga?
Esto Cid, ¿significa lo que expongo arriba o lo he malinterpretado?.
ResponderBorrar"sino también todo el poder maléfico acumulado por la comunidad y la nación a las cuales pertenece, ya que él es parte integrante de esos agregados y lo que influencia al ser humano individual o a la colectividad (ciudad o nación), repercute también sobre él."
Estaría bien esa iniciativa si es a lo que se refiere el artículo?
ResponderBorrarAsí como yo lo comprendí, lo que quiso decir Blavatsky es que cuando te esmeras con intensidad y tenacidad para perfeccionarte para de esta forma poderte volver un discípulo de los maestros. No solamente vas a tener que confrontarte con tu “antiguo yo” quien no quiere salir de su zona de conformidad, sino que también te vas a tener que confrontar con el egregor de la colectividad en la que vives, o sea la entidad energética que las personas han creado inconscientemente a través de sus acciones, y esta entidad no quiere que las cosas cambien porque su existencia depende que todo siga igual.
BorrarEn cuanto a encarar a la población para tratar de hacerla despertar, yo no lo recomiendo porque eso solo lo van a tomar como una agresión, en cambio pienso que es mejor esperar el momento adecuado para ir despertando a las personas de manera más puntual.
Oye cid por curiosidad tu si quieres salir del ciclo de encarnaciones entonces vas en dirección a ser un pratyeka buddha?
BorrarTanto el Buda egoísta como el Buda de compasión se liberan del ciclo de las reencarnaciones, la diferencia es que el primero entra en el Nirvana mientras que el segundo permanece en el universo manifestado para poder seguir ayudando a los humanos.
BorrarY aunque yo quisiera liberarme del ciclo de las reencarnaciones, todavía estoy muy lejos de poder alcanzar el nivel de desarrollo que me permitiría lograr eso